Was ist das Bitcoin Whitepaper?
Am 31. Oktober 2008 veröffentlichte eine Person mit dem Namen Satoshi Nakamoto auf metzdowd.com das “Bitcoin P2P e-cash paper”.
Dieses Dokument handelt von einer neuen Form von elektronischem Bargeld, die Peer-to-Peer ist und keine Drittpartei benötigt.
Der angehängte Link führt zu einem PDF, das heute als das Bitcoin-Whitepaper bzw. Bitcoin White Paper bekannt ist. Dieses enthält Grundidee und technologische Details für die Umsetzung von Bitcoin.
Bitcoin Whitepaper als Download
Du kannst das Dokument auf Deutsch oder Englisch herunterladen. BitcoinBasis hat die englische Fassung übersetzt. Diese steht dir als Download oder unterhalb als Text zur Verfügung.
Bitcoin-Whitepaper: Original (PDF)
Bitcoin Whitepaper (Original | Englisch)
Bitcoin-Whitepaper: Deutsch (PDF)
Bitcoin Whitepaper (Deutsch | Übersetzt)
Bitcoin Whitepaper auf Deutsch
Bitcoin: Ein Peer-to-Peer-Electronic-Cash-System
Satoshi Nakamoto
satoshin@gmx.com
www.bitcoin.org
übersetzt von BitcoinBasis.de
Abstrakt. Eine reine Peer-to-Peer-Version von Electronic Cash würde es ermöglichen, Online-Zahlungen direkt von einer Partei zur anderen zu senden, ohne ein Finanzinstitut einzuschalten. Digitale Signaturen sind ein Teil der Lösung, aber die Hauptvorteile, nämlich die Vermeidung von Doppelausgaben, gehen verloren, wenn ein treuhänderischer Dritter weiterhin benötigt wird. Wir schlagen eine Lösung für das Problem der Doppelausgaben durch den Einsatz eines Peer-to-Peer-Netzwerks vor. Das Netzwerk kennzeichnet Transaktionen mit einem Zeitstempel, indem es sie in eine fortlaufende Kette von hash-basierten Proofs-of-Work (Arbeitsnachweisen) einfügt, die einen Datensatz bilden, der nicht geändert werden kann, ohne den Proof-of-Work erneut durchzuführen. Die längste Kette dient nicht nur als Beweis für den Ablauf der beobachteten Ereignisse, sondern auch als Nachweis dafür, dass sie aus dem größten Pool an CPU-Leistung stammt. Solange ein Großteil der CPU-Leistung von Knoten kontrolliert wird, die nicht bei einem Angriff auf das Netzwerk kooperieren, werden sie die längsten Ketten erzeugen und schneller als Angreifer sein. Das Netzwerk selbst erfordert nur eine minimale Struktur. Nachrichten werden nach bestem Wissen und Gewissen gesendet, und die Knoten können das Netzwerk nach Belieben verlassen und wieder betreten. Dabei nehmen sie die längste Proof-of-Work-Kette als Nachweis für die Ereignisse an, die während ihrer Abwesenheit geschehen sind.
1. Einführung
Der Handel im Internet ist fast ausschließlich auf Finanzinstitute angewiesen, die als treuhänderische Dritte für die Abwicklung elektronischer Zahlungen fungieren. Obwohl das System für die meisten Transaktionen gut genug funktioniert, leidet es doch unter den inhärenten Schwächen des treuhandbasierten Modells. Es ist nicht möglich, Transaktionen wirklich rückgängig zu machen, da Finanzinstitute unvermeidlich als Mediatoren bei Unstimmigkeiten fungieren. Die Kosten der Mediation erhöhen die Transaktionskosten, setzen praktische Untergrenzen für die Höhe der Transaktionen und unterbinden die Möglichkeit kleinerer informeller Transaktionen. Es entstehen höhere Kosten durch die mangelnde Fähigkeit, nicht rückgängig zu machende Zahlungen für nicht rückgängig zu machende Dienstleistungen auszuführen. Mit der Möglichkeit des Rückgängigmachens wächst der Bedarf an Vertrauen. Händler müssen sich vor ihren Kunden in Acht nehmen und mehr Informationen abfragen, als sie eigentlich benötigen. Eine bestimmtere Betrugsquote wird als unvermeidbar akzeptiert. Diese Kosten und Zahlungsunsicherheiten können persönlich durch die Verwendung von Bargeld vermieden werden, aber es gibt keinen Mechanismus, um Zahlungen über einen Kommunikationskanal ohne eine treuhänderische Partei durchzuführen.
Benötigt wird ein elektronisches Zahlungssystem, das auf kryptographischen Nachweisen statt auf Vertrauen basiert und es zwei abschlusswilligen Parteien ermöglicht, direkt miteinander zu handeln, ohne dass ein treuhänderischer Dritter erforderlich ist. Transaktionen, die durch Rechnervorgänge nicht rückgängig zu machen sind, würden die Verkäufer vor Betrug schützen, und routinemäßige Treuhandmechanismen könnten leicht implementiert werden, um die Käufer zu schützen. In diesem Papier schlagen wir eine Lösung für das Problem der doppelten Ausgaben vor, indem wir einen Peer-to-Peer verteilten Zeitstempel-Server verwenden, um einen rechnerischen Nachweis der chronologischen Reihenfolge der Transaktionen zu generieren. Das System ist sicher, solange redliche Knoten gemeinsam mehr CPU-Leistung kontrollieren als jede kooperierende Gruppe von Angreifern.
2. Transaktionen
Wir definieren eine elektronische Münze als eine Kette von digitalen Signaturen. Ein Inhaber der Münze übergibt sie an den nächsten, indem er einen Hash der vorherigen Transaktion und den öffentlichen Schlüssel des nächsten Besitzers digital signiert und diese am Ende der Münze anfügt. Ein Zahlungsempfänger kann die Signaturen überprüfen, um die Eigentümerstruktur zu verifizieren.
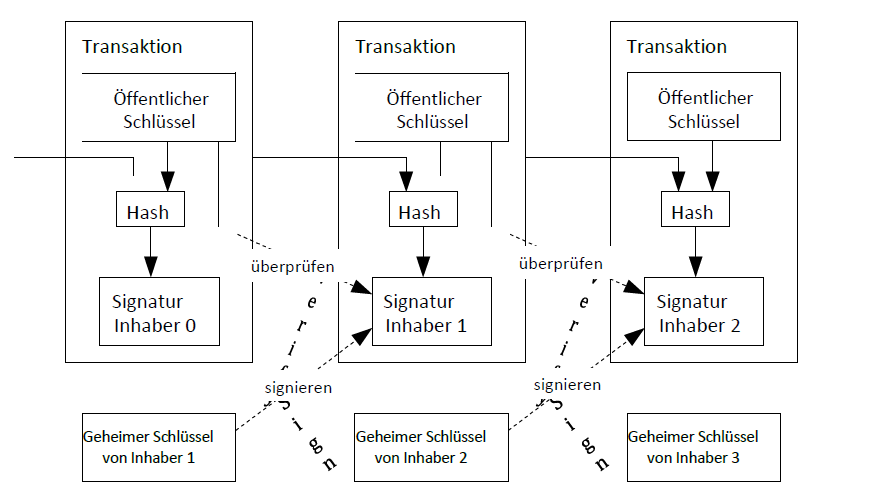
Das Problem ist natürlich, dass der Zahlungsempfänger nicht überprüfen kann, ob einer der Inhaber die Münze nicht doppelt ausgegeben hat. Eine übliche Lösung besteht darin, eine zentrale treuhänderische Stelle oder Münzanstalt („Mint“) einzuschalten, die jede Transaktion auf doppelte Ausgaben überprüft. Nach jeder Transaktion muss die Münze an die Münzanstalt zurückgegeben werden, die eine neue Münze ausgibt, und nur direkt von der Münzanstalt ausgegebene Münzen genießen das Vertrauen, dass sie nicht doppelt ausgegeben wurden. Das Problem bei dieser Lösung ist, dass das Schicksal des gesamten Geldsystems von Betreiber der Münzanstalt abhängt, wobei jede Transaktion durch sie laufen muss, genau wie bei einer Bank.
Wir brauchen eine Möglichkeit, den Zahlungsempfänger wissen zu lassen, dass die Vorbesitzer keine früheren Transaktionen signiert haben. In diesem Sinne ist die früheste Transaktion ausschlaggebend, sodass uns spätere Versuche, die Münze doppelt auszugeben, nicht interessieren. Die Überprüfung, dass keine Transaktion fehlt, kann nur stattfinden, wenn alle Transaktionen bekannt sind. Im Münzanstalt-Modell kannte die Münzanstalt alle Transaktionen und entschied, welche zuerst eintrafen. Um dies ohne treuhänderische Partei zu erreichen, müssen Transaktionen öffentlich bekannt gemacht werden[1] und wir brauchen ein System, in dem sich die Teilnehmer auf eine einheitliche Historie der Eingangsreihenfolge einigen können. Der Zahlungsempfänger benötigt einen Nachweis, dass zum Zeitpunkt einer Transaktion die Mehrheit der Knoten zugestimmt hat, dass sie als erste eingegangen ist.
3. Zeitstempel-Server
Die von uns vorgeschlagene Lösung beginnt mit einem Zeitstempelserver. Ein Zeitstempel-Server nimmt einen Hash aus einem Block von Elementen, die mit einem Zeitstempel versehen werden sollen, und veröffentlicht den Hash, z.B. in einer Zeitung oder einem Usenet-Post[2-5]. Der Zeitstempel weist nach, dass die Daten zu diesem Zeitpunkt offensichtlich vorhanden gewesen sein müssen, sonst könnten sie nicht in den Hash gelangen. Jeder Zeitstempel enthält den vorherigen Zeitstempel in seinem Hash und bildet eine Kette, wobei jeder zusätzliche Zeitstempel die davor liegenden bekräftigt.
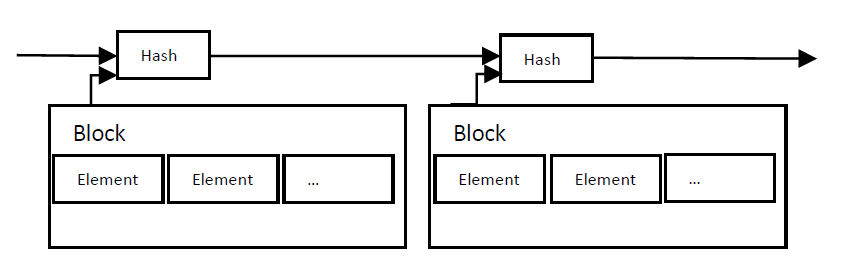
4. Proof-of-Work
Um einen dezentralen Zeitstempelserver auf Peer-to-Peer-Basis zu implementieren, müssen wir statt Zeitungsanzeigen oder Usenet-Posts ein Proof-of-Work-System ähnlich Adam Backs Hashcash[6] verwenden. Der Proof-of-Work enthält das Durchsuchen nach einem Wert, bei dem der Hash anfänglich, z.B. bei SHA-256, mit einer Anzahl von Nullbits beginnt. Der durchschnittliche Arbeitsaufwand ist exponentiell in Bezug auf die Anzahl der erforderlichen Nullbits und kann durch Ausführen eines einzelnen Hashs überprüft werden.
Für unser Zeitstempelnetzwerk implementieren wir den Proof-of-Work durch Inkrementieren eines Nonce im Block, bis ein Wert gefunden wird, der dem Hash des Blocks die erforderlichen Nullbits gibt. Sobald der CPU-Aufwand für den Proof-of-Work geleistet wurde, kann der Block nicht mehr geändert werden, ohne die Arbeit erneut zu erledigen. Da spätere Blöcke danach verkettet werden, würde ein Ändern des Blocks das Wiederholen aller nachfolgenden Blöcke bedeuten.
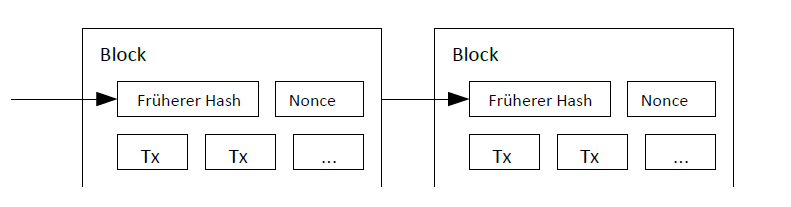
Der Proof-of-Work löst auch das Problem der Bestimmung der Vertretungsbefugnis bei Mehrheitsentscheidungen. Wenn die Mehrheit auf einer IP-Adresse – einer Stimme – beruhen würde, könnte sie von jedem, der in der Lage ist, viele IPs zu vergeben, untergraben werden. Der Proof-of-Work folgt dem Grundsatz: eine CPU – eine Stimme. Die Mehrheitsentscheidung wird durch die längste Kette vertreten, die den größten Proof-of-Work-Aufwand hat. Wenn eine Mehrheit der CPU-Leistung von redlichen Knoten gesteuert wird, wird die redliche Kette am schnellsten wachsen und alle konkurrierenden Ketten hinter sich lassen. Um einen früheren Block zu modifizieren, müsste ein Angreifer den Proof-of-Work des Blocks und aller nachfolgenden Blöcke erneut durchführen und dann die Arbeit der redlichen Knoten einholen und überholen. Wir werden später zeigen, dass die Wahrscheinlichkeit, dass ein langsamerer Angreifer aufholt, exponentiell abnimmt, wenn nachfolgende Blöcke hinzugefügt werden.
Um das steigende Hardware-Tempo und das sich im Laufe der Zeit verändernde Interesse an der Ausführung von Knoten zu kompensieren, wird die Schwierigkeit des Proof-of-Work durch einen gleitenden Durchschnitt bestimmt, der auf eine durchschnittliche Anzahl von Blöcken pro Stunde abzielt. Wenn sie zu schnell erzeugt werden, steigt der Schwierigkeitsgrad.
5. Netzwerk
Das Ausführen des Netzwerks erfolgt in folgenden Schritten:
1) Neue Transaktionen werden an alle Knoten gesendet.
2) Jeder Knoten sammelt neue Transaktionen zu einem Block.
3) Jeder Knoten arbeitet daran, einen schwierigen Proof-of-Work für seinen Block zu finden.
4) Wenn ein Knoten einen Proof-of-Work findet, sendet er den Block an alle Knoten.
5) Die Knoten akzeptieren den Block nur, wenn alle darin enthaltenen Transaktionen gültig sind und noch nicht ausgegeben wurden.
6) Die Knoten stellen ihre Akzeptanz des Blocks fest, indem sie daran arbeiten, den nächsten Block in der Kette zu erstellen, indem sie den Hash des akzeptierten Blocks als vorherigen Hash verwenden.
Die Knoten halten immer die längste Kette für die richtige und werden weiter daran arbeiten, sie zu erweitern. Wenn zwei Knoten gleichzeitig verschiedene Versionen des nächsten Blocks senden, können einige Knoten zuerst den einen oder den anderen empfangen. In diesem Fall arbeiten sie an dem ersten, den sie erhalten haben, aber speichern den anderen Ast, falls er länger wird. Die Verkettung wird unterbrochen, wenn der nächste Proof-of-Work gefunden und ein Ast länger wird; die Knoten, die am anderen Ast gearbeitet haben, wechseln dann zum längeren.
Neue Transaktionsübertragungen müssen nicht unbedingt alle Knoten erreichen. Solange sie viele Knoten erreichen, werden sie rasch in einen Block geraten. Blockübertragungen sind auch tolerant gegenüber ausgelassenen Messages. Wenn ein Knoten keinen Block empfängt, wird er ihn anfordern, wenn er den nächsten Block empfängt und feststellt, dass er einen ausgelassen hat.
6. Anreiz
Es gilt die Konvention, dass die erste Transaktion in einem Block eine spezielle Transaktion ist, die eine neue Münze startet, die dem Schöpfer des Blocks gehört. Dies schafft einen Anreiz für die Knoten, das Netzwerk zu unterstützen, und bietet die Möglichkeit, dem Umlauf von Münzen zu starten, da es keine zentrale Stelle gibt, die sie ausgibt. Die stetige Hinzufügung einer konstanten Menge an neuen Münzen ist analog zu Goldgräbern, die Ressourcen aufwenden, um Gold in Umlauf zu bringen. In unserem Fall besteht der Ressourcenaufwand in CPU-Zeit und Strom.
Der Anreiz kann auch mit Transaktionsgebühren finanziert werden. Wenn der Output einer Transaktion weniger wert ist als der Input, ist die Differenz eine Transaktionsgebühr, die zum Anreizwert des Blocks, der die Transaktion enthält, addiert wird. Sobald eine vorbestimmte Anzahl von Münzen in Umlauf gelangt ist, kann der Anreiz vollständig auf Transaktionsgebühren umgestellt werden und ist völlig inflationsfrei.
Der Anreiz kann dazu beitragen, dass die Knoten redlich bleiben. Wenn ein gieriger Angreifer in der Lage ist, mehr CPU-Leistung als alle redlichen Knoten zu sammeln, müsste er sich entscheiden, ob er dadurch betrügt, indem er seine Zahlungen zurückstiehlt, oder ob er sie zum Erzeugen neuer Münzen verwendet. Er dürfte es für profitabler halten, sich an die Regeln zu halten, weil diese Regeln ihn mit mehr neuen Münzen begünstigen, als alle anderen zusammen, als das System und die Gültigkeit seines eigenen Vermögens zu untergraben.
7. Neubelegen von Festplattenspeicherplatz
Sobald die letzte Transaktion in einer Münze unter genügend Blöcken vergraben ist, können die vorher verbrauchten Transaktionen verworfen werden, um Speicherplatz zu sparen. Um dies zu ermöglichen, ohne den Hash des Blocks zu brechen, werden Transaktionen („Tx“) in einem Hash-Baum[7][2][5] gehasht, wobei nur der Root-Hash in den Hash des Blocks aufgenommen wird. Alte Blöcke können dann durch Abschneiden von Ästen des Baumes verdichtet werden. Die inneren Hashes brauchen nicht gespeichert zu werden.

Ein Block-Header ohne Transaktionen würde etwa 80 Byte groß sein. Wenn wir annehmen, dass alle 10 Minuten Blöcke generiert werden, sind das 80 Bytes * 6 * 24 * 365 = 4,2 MB pro Jahr. Da Computersysteme ab 2008 typischerweise mit 2 GB RAM auf den Markt kommen, und laut dem mooreschen Gesetz, das ein laufendes Wachstum von 1,2 GB pro Jahr prognostiziert, dürfte die Speicherung kein Problem darstellen, selbst wenn die Block-Header im Speicher verbleiben müssen.
8. Vereinfachte Zahlungsüberprüfung
Es ist möglich, Zahlungen zu überprüfen, ohne einen vollständigen Netzwerkknoten zu betreiben. Ein Benutzer muss nur eine Kopie der Block-Header der längsten Proof-of-Work-Kette aufbewahren, die er durch Abfragen von Netzwerkknoten erhalten kann, bis er überzeugt ist, dass er die längste Kette hat, und den Ast des Hash-Baums erhalten, der die Transaktion mit dem Block verknüpft, in dem sie sich mit Zeitstempel befindet. Er kann die Transaktion nicht selbst überprüfen, aber indem er sie mit einer Stelle in der Kette verknüpft, kann er sehen, dass ein Netzwerkknoten sie akzeptiert hat. Später hinzugefügte Blöcke bestätigen weiter, dass das Netzwerk sie akzeptiert hat.

Im Prinzip ist die Überprüfung zuverlässig, solange redliche Knoten das Netzwerk kontrollieren, aber sie ist anfälliger, wenn das Netzwerk von einem Angreifer überlastet wird. Während Netzwerkknoten Transaktionen selbst verifizieren können, kann die vereinfachte Methode durch gefälschte Transaktionen eines Angreifers getäuscht werden, solange der Angreifer das Netzwerk weiterhin überlasten kann. Eine Strategie, um sich davor zu schützen, wäre es, Warnungen von Netzwerkknoten zu akzeptieren, wenn sie einen ungültigen Block erkennen, und die Software des Benutzers aufzufordern, den vollständigen Block und sowie Transaktionen mit Alarmen herunterzuladen, um die Inkonsistenz zu bestätigen. Unternehmen, die häufige Zahlungen erhalten, werden wahrscheinlich weiterhin ihre eigenen Knoten betreiben wollen, um eine unabhängigere Sicherheit und schnellere Verifizierung zu gewährleisten.
9. Kombination und Teilung des Wertes
Obwohl es möglich wäre, Münzen einzeln zu behandeln, wäre es schwierig, für jeden Cent einer Überweisung eine separate Transaktion durchzuführen. Um eine Aufteilung und Kombination von Werten zu ermöglichen, enthalten Transaktionen mehrere Inputs und Outputs. Normalerweise gibt es entweder einen einzigen Input aus einer größeren früheren Transaktion oder mehrere Inputs, die kleinere Beträge zusammenfassen, und höchstens zwei Outputs: einen für die Zahlung und gegebenenfalls einen für die Quittierung der Änderung an den Absender.

Es ist zu beachten, dass das Fan-Out (Ausfächerung), bei dem eine Transaktion von mehreren Transaktionen abhängt und diese Transaktionen von viel mehr abhängen, hier kein Problem darstellt. Es besteht nie die Notwendigkeit, eine vollständige eigenständige Ausfertigung der Transaktionshistorie zu extrahieren.
10. Datenschutz
Das traditionelle Bankenmodell erreicht ein hohes Maß an Datenschutz, indem es den Zugang zu Informationen auf die beteiligten Parteien und den treuhänderischen Dritten beschränkt. Die Notwendigkeit, alle Transaktionen öffentlich bekannt zu machen, schließt diese Methode aus, aber die Privatsphäre kann dennoch gewahrt werden, indem der Informationsfluss an einem anderen Ort unterbrochen wird: durch die Anonymisierung öffentlicher Schlüssel. Es kann öffentlich gesehen werden, dass jemand einen Betrag an jemand anderen sendet, aber ohne Angaben zur Verbindung der Transaktionen mit einer Person. Dies ähnelt dem Informationsstand an Börsen, wo Zeit und Umfang der einzelnen Geschäfte, das „Band“, veröffentlicht werden, ohne jedoch zu sagen, wer die Parteien waren.

Als zusätzliche Firewall sollte für jede Transaktion ein neues Schlüsselpaar verwendet werden, damit sie nicht mit einem gemeinsamen Inhaber verbunden werden. Einige Verknüpfungen sind bei Multi-Input-Transaktionen immer noch unvermeidlich, was zwangsläufig darauf hindeutet, dass ihre Inputs demselben Inhaber gehörten. Das Risiko besteht darin, dass, wenn der Inhaber eines Schlüssels aufgedeckt wird, die Verknüpfung andere Transaktionen aufdecken könnte, die zum gleichen Inhaber gehörten.
11. Berechnungen
Wir berücksichtigen ein Szenario, in dem ein Angreifer versucht, eine alternative Kette schneller zu generieren als die redliche Kette. Selbst wenn dies erreicht wird, öffnet es das System nicht für willkürliche Änderungen, wie z.B. die Schaffung von Mehrwert aus dem Nichts oder die Entnahme von Geld, das nie dem Angreifer gehörte. Die Knoten werden eine ungültige Transaktion nicht als Zahlung akzeptieren, und redliche Knoten werden niemals einen Block mit ihnen akzeptieren. Ein Angreifer kann nur versuchen, eine seiner eigenen Transaktionen zu ändern, um Geld zurückzuholen, das er kürzlich ausgegeben hat.
Das Rennen zwischen der redlichen Kette und einer Angreiferkette kann als binomiale Irrfahrt oder Random-Walk bezeichnet werden. Das Erfolgsereignis ist, dass die redliche Kette um einen Block verlängert wird, wodurch ihr Vorsprung um +1 erhöht wird, und das Misserfolgserereignis ist, dass die Kette des Angreifers um einen Block verlängert und der Abstands um -1 verkürzt wird.
Die Wahrscheinlichkeit, dass ein Angreifer aus einem bestimmten Defizit aufholt, entspricht der Ruinwahrscheinlichkeit eines Spielers. Angenommen, ein Spieler mit unbegrenztem Guthaben beginnt mit einem Defizit und spielt potenziell eine unendliche Anzahl von Versuchen, um den Break-even zu erreichen. Die Wahrscheinlichkeit, dass er jemals den Break-even erreicht oder dass ein Angreifer die redliche Kette einholt, lässt sich wie folgt berechnen[8]:
p = Wahrscheinlichkeit, dass ein redlicher Knoten den nächsten Block findet
q = Wahrscheinlichkeit, dass der Angreifer den nächsten Block findet
qz = Wahrscheinlichkeit, dass der Angreifer jemals z Blöcke hinter sich aufholen wird

Unter der Annahme, dass p > q, sinkt die Wahrscheinlichkeit exponentiell, wenn die Anzahl der Blöcke, die der Angreifer nachholen muss, zunimmt. Wenn er nicht schon früh einen glücklichen Sprung nach vorne macht, stehen die Chancen gegen ihn und seine Chancen werden verschwindend gering, wenn er weiter zurückfällt.
Wir überlegen nun, wie lange der Empfänger einer neuen Transaktion warten muss, bis er sicher ist, dass der Absender die Transaktion nicht ändern kann. Wir gehen davon aus, dass der Absender ein Angreifer ist, der den Empfänger glauben machen will, dass er ihn für eine Weile bezahlt hat, und nach einiger umschwenkt und an sich selbst zurückzahlt. Der Empfänger wird gewarnt, wenn dies geschieht, aber der Absender hofft, dass es zu spät ist.
Der Empfänger erzeugt ein neues Schlüsselpaar und übergibt den öffentlichen Schlüssel kurz vor der Signierung an den Absender. Dies verhindert, dass der Absender eine Kette von Blöcken vorzeitig vorbereitet, indem er kontinuierlich daran arbeitet, bis er das Glück hat, weit genug voraus zu sein, und dann die Transaktion in diesem Moment ausführt. Sobald die Transaktion gesendet wurde, beginnt der unredliche Absender, heimlich an einer parallelen Kette zu arbeiten, die eine alternative Version seiner Transaktion enthält.
Der Empfänger wartet, bis die Transaktion zu einem Block hinzugefügt wurde und danach z Blöcke verknüpft wurden. Er weiß nicht genau, wie viel Fortschritt der Angreifer gemacht hat, aber unter der Annahme, dass die ehrlichen Blöcke die durchschnittlich erwartete Zeit pro Block benötigt haben, wird der potenzielle Fortschritt des Angreifers eine Poisson-Verteilung sein, wobei der erwartete Wert ist:
λ = z q/p
Um die Wahrscheinlichkeit zu erhalten, dass der Angreifer jetzt noch aufholen könnte, multiplizieren wir die Dichte der Poisson-Verteilung für jede Menge Fortschritt, die er hätte machen können, mit der Wahrscheinlichkeit, dass er von diesem Punkt an aufholen könnte:
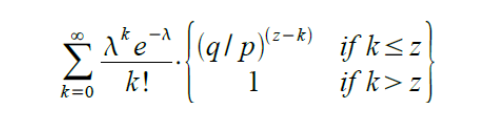
Umordnen, um die Summierung des unendlichen Tails der Verteilung zu vermeiden…

Umwandlung in C-Code …
#include <math.h>
double AttackerSuccessProbability(double q, int z)
{
double p = 1.0 – q;
double lambda = z * (q / p);
double sum = 1.0;
int i, k;
for (k = 0; k <= z; k++)
{
double poisson = exp(-lambda);
for (i = 1; i <= k; i++)
poisson *= lambda / i;
sum -= poisson * (1 – pow(q / p, z – k));
}
return sum;
}
Nach einigen Ergebnisläufen können wir den Wahrscheinlichkeitsabfall exponentiell mit z sehen.
q=0.1
z=0 P=1.0000000
z=1 P=0.2045873
z=2 P=0.0509779
z=3 P=0.0131722
z=4 P=0.0034552
z=5 P=0.0009137
z=6 P=0.0002428
z=7 P=0.0000647
z=8 P=0.0000173
z=9 P=0.0000046
z=10 P=0.0000012
q=0.3
z=0 P=1.0000000
z=5 P=0.1773523
z=10 P=0.0416605
z=15 P=0.0101008
z=20 P=0.0024804
z=25 P=0.0006132
z=30 P=0.0001522
z=35 P=0.0000379
z=40 P=0.0000095
z=45 P=0.0000024
z=50 P=0.0000006
Lösen für P kleiner als 0,1% …
P < 0.001
q=0.10 z=5
q=0.15 z=8
q=0.20 z=11
q=0.25 z=15
q=0.30 z=24
q=0.35 z=41
q=0.40 z=89
q=0.45 z=340
12. Fazit
Wir haben ein System für elektronische Transaktionen vorgeschlagen, ohne auf Treuhandschaft angewiesen zu sein. Wir haben mit dem üblichen Rahmen von Münzen aus digitalen Signaturen begonnen, der eine starke Kontrolle der Inhaberschaft ermöglicht, aber ohne eine Möglichkeit zur Vermeidung von Doppelausgaben unvollständig bleibt. Um dies zu lösen, schlugen wir ein Peer-to-Peer-Netzwerk mit Proof-of-Work vor, um eine öffentliche Historie der Transaktionen aufzuzeichnen, die für einen Angreifer schnell rechentechnisch unpraktisch wird, wenn redliche Knoten einen Großteil der CPU-Leistung kontrollieren. Das Netzwerk ist robust in seiner unstrukturierten Einfachheit. Alle Knoten funktionieren gleichzeitig mit wenig Koordination. Sie müssen nicht identifiziert werden, da Messages nicht an einen bestimmten Ort weitergeleitet werden und nur nach dem Best-Effort-Prinzip geliefert werden müssen. Die Knoten können das Netzwerk nach Belieben verlassen und wieder eintreten, indem sie die Proof-of-Work-Kette als Beweis dafür akzeptieren, was geschehen ist, während sie weg waren. Sie stimmen mit ihrer CPU-Leistung ab und drücken ihre Akzeptanz gültiger Blöcke aus, indem sie an deren Erweiterung arbeiten und ungültige Blöcke ablehnen, indem sie sich weigern, an ihnen zu arbeiten. Alle erforderlichen Regeln und Anreize können mit diesem Konsens-Mechanismus durchgesetzt werden.
Referenzen
[1] W. Dai, „b-money,“ http://www.weidai.com/bmoney.txt, 1998.
[2] H. Massias, X.S. Avila, and J.-J. Quisquater, „Design of a secure timestamping service with minimal trust requirements,“ In 20th Symposium on Information Theory in the Benelux, May 1999.
[3] S. Haber, W.S. Stornetta, „How to time-stamp a digital document,“ In Journal of Cryptology, vol 3, no 2, pages 99-111, 1991.
[4] D. Bayer, S. Haber, W.S. Stornetta, „Improving the efficiency and reliability of digital time-stamping,“ In Sequences II: Methods in Communication, Security and Computer Science, pages 329-334, 1993.
[5] S. Haber, W.S. Stornetta, „Secure names for bit-strings,“ In Proceedings of the 4th ACM Conference on Computer and Communications Security, pages 28-35, April 1997.
[6] A. Back, „Hashcash – a denial of service counter-measure,“ http://www.hashcash.org/papers/hashcash.pdf, 2002.
[7] R.C. Merkle, „Protocols for public key cryptosystems,“ In Proc. 1980 Symposium on Security and Privacy, IEEE Computer Society, pages 122-133, April 1980.
[8] W. Feller, „An introduction to probability theory and its applications,“ 1957
Häufige Fragen zum Bitcoin Whitepaper
Wann wurde das Bitcoin Whitepaper veröffentlicht?
Satoshi Nakamoto veröffentlichte am 31. Oktober 2008 das „Bitcoin P2P e-cash paper“, das heute als das Bitcoin Whitepaper bekannt ist.
❔ Gibt es das Bitcoin Whitepaper auch auf Deutsch?
Die Originalsprache des Bitcoin Whitepapers ist englisch. BitcoinBasis hat das Dokument übersetzt und für jeden zum Download zur Verfügung gestellt.







